Einführung in die binomischen Formeln

1 Startseite

Lernziel

In diesem Kurs lernst du die binomischen Formeln kennen.

Voraussetzungen

Was passiert in diesem Kurs

Hier hast du einen Überblick, wie dieser Kurs genau abläuft. Du kannst damit deinen eigenen Lehrplan machen.

Warum sollte man die binomischen Formeln kennen?
Herleitung der drei Binomischen Formeln mit geometrischer Veranschaulichung
Aufgaben zum Üben
Zusammenfassung

Artikel zum Kurs

Den theoretischen Inhalt des Kurses kannst du im Artikel binomische Formeln nachlesen.

2 Warum sollte man die binomischen Formeln kennen?

Die binomischen Formeln erleichtern das Ausmultiplizieren von Klammern. Sie ergeben sich aus den bereits bekannten Rechenregeln für Terme mit Klammern, machen aber die Rechnung kürzer.

Zum Beispiel: Multipliziere diesem Term $(x+3)\cdot(x+3)$ aus.

Mit binomischen Formeln kann man solche langen Rechnungen in einem Schritt lösen.

Wir werden im Folgenden die drei binomischen Formeln herleiten.

3 Herleitung der 1. binomischen Formel

Im Prinzip ist die Herleitung der binomischen Formeln nichts anderes als Klammern ausmultiplizieren.

1. binomische Formel

Im Beispiel der ersten binomischen Formel beginnt man mit dem Ausgangsterm

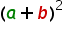
und schreibt die Potenz aus.

Nun multipliziert man nacheinander die Klammern aus, wie schematisch dargestellt:

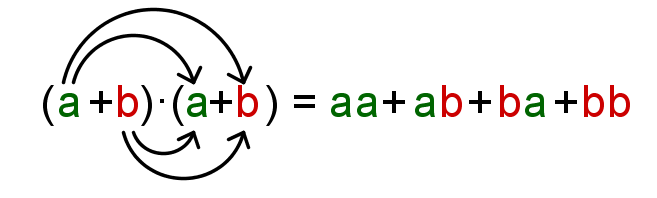
Mit Kommutativgesetz erhält man die endgültige Form:

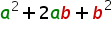
Diesen Term lernt man auswendig. Dann kann man die Lösung direkt hinschreiben.

4 Anschauliche Erklärung der 1. binomischen Formel

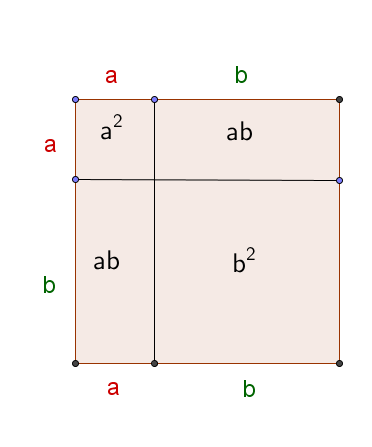
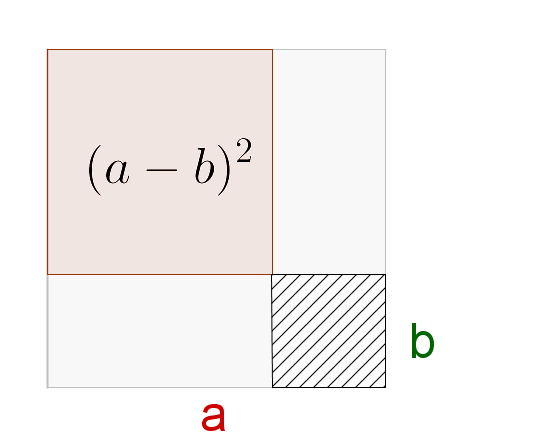
Auf der vorherigen Seite hast du kennengelernt, wie man die 1. binomischen Formel algebraisch durch Ausmultiplizieren herleitet. Es gibt aber noch die Möglichkeit, die Formel durch Flächenvergleiche herzuleiten. Das funktioniert so:

Der Flächeninhalt des großen Quadrats ist $\left(a+b\right)^2$ und damit gleich dem Ergebnis der 1. binomischen Formel.

An der Zeichnung sieht man, dass sich das Quadrat aus vier Teilflächen zusammensetzt. Diese haben die Flächeninhalte $a^{2}, a b, a b, b^{2}$ .

Die Fläche des Quadrats ergibt sich als Summe der Teilflächen:

$\Rightarrow (a+b)^2=a^2+ ab+ab+b^2=a^2+ 2 a b+b^2$

Das ist gerade die 1. binomischen Formel.

5 Herleitung der 2. binomischen Formel

Im Prinzip ist die Herleitung der binomischen Formeln nichts anderes als Klammern ausmultiplizieren.

2. binomische Formel

Die Herleitung der zweiten Formel läuft ähnlich. Beginnend mit

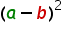
schreibt man die Potenz aus.

und multipliziert dem Schema folgend aus. Beachte dabei beim letzten Produkt, dass $\left(-b\right)\cdot\left(-b\right)=+bb$ gilt:

Mit Kommutativgesetz erhält man wieder die endgültige Form:

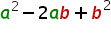
Diesen Term lernt man wieder auswendig. Beachte dabei, dass er sich vom Ergebnis der 1. binomischen Formel nur durch das Minus in der Mitte unterscheidet. Die Lösung kann man dann wieder direkt hinschreiben.

6 Anschauliche Erklärung der 2. binomischen Formel

Man geht von der rechten Seite der Gleichung aus und versucht aus dem gesamten Quadrat mit Flächeninhalt $a^{2}$ das kleine Quadrat mit Flächeninhalt $(a - b)^{2}$ zu bekommen.

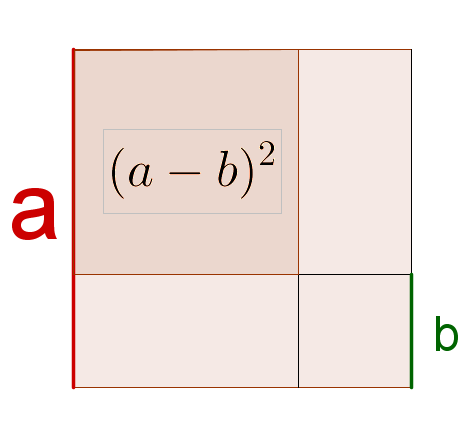
Das gesamte Quadrat hat den Flächeninhalt $a^{2}$ . Man zieht davon zuerst das schraffierte Rechteck ab. Der Rest (rosa Fläche) hat nun den Flächeninhalt $a^{2} - a b$

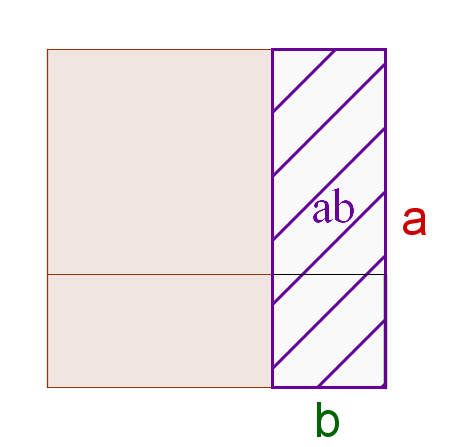
Nun zieht man zusätzlich diese schraffierte Fläche ab. Wir erhalten als Flächeninhalt $a^{2} - 2 a b$ .

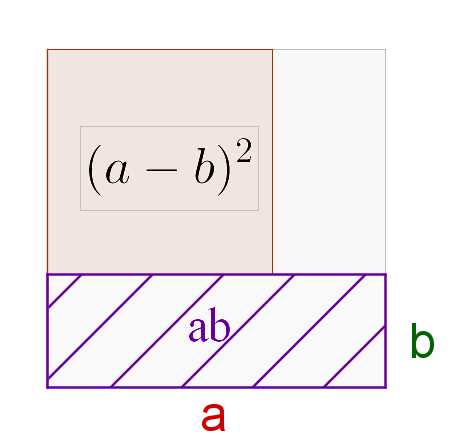
Allerdings haben wir das Quadrat unten rechts mit dem Flächeninhalt $b^{2}$ einmal zu viel abgezogen, sodass die Fläche wieder dazu gezählt werden muss.

Damit bekommt man die Fläche mit dem Flächeninhalt $(a - b)^{2}$ .

Insgesamt erhalten wir also für den Flächeninhalt:

\displaystyle (a-b)^2=a^2-2ab+b^2

Das ist die 2. binomische Formel.

7 Herleitung der 3. binomischen Formel

Auch die 3. binomische Formel ist ein Sonderfall von "Klammer mal Klammer". Die Technik dafür kannst du hier nochmal nachlesen bzw. üben.

Die Ausgangsformel ist diesmal

Jetzt multiplizieren wir aus:

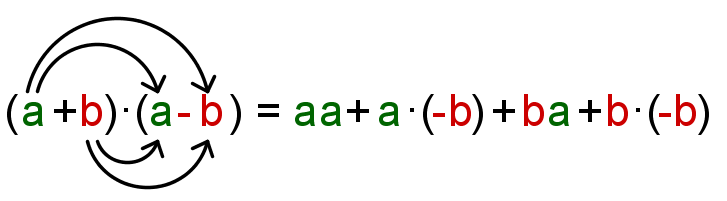
Nun können wir die Minus-Zeichen vorziehen.

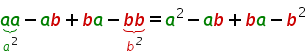
Insgesamt erhalten wir:

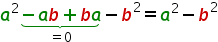
Auch diese Formel lernt man wieder auswendig und kann dann die Lösung direkt angeben.

8 Anschauliche Erklärung der 3. binomischen Formel

Das große Quadrat hat den Flächeninhalt $a^{2}$ . Versuche daraus ein Rechteck mit Flächeninhalt $(a - b) (a + b)$ zu bekommen.

Man zeichnet nun ein Quadrat unten rechts mit dem Flächeninhalt $b^{2}$ . Das schraffierte Rechteck darüber, mit den Seitenlängen $b$ und $(a - b)$ schneidet man aus und legt es an die rote Fläche unten an.

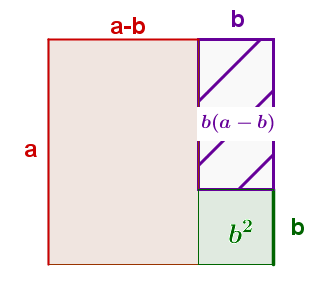
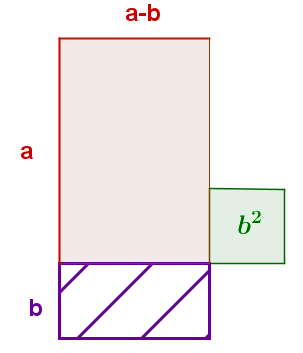
Das rote und das lila schraffierte Rechteck zusammen haben den Flächeninhalt $(a + b) (a - b)$ . Zusätzlich gibt es immer noch das kleine, grüne Quadrat mit dem Flächeninhalt $b^{2}$ .

Da nur das lila schraffierte Rechteck verschoben wurde, hat sich der gesamte Flächeninhalt nicht verändert. Damit ergibt sich der Flächeninhalt: $(a + b) (a - b) + b^{2}$

Deshalb gilt: $a^{2} = (a + b) (a - b) + b^{2}$

Wenn man nun $b^{2}$ auf beiden Seiten subtrahiert, erhält man die 3. binomische Formel:

$a^{2} - b^{2} = (a + b) (a - b)$

9 Übungsaufgaben

Laden

Weitere Aufgaben findest du im Ordner Aufgaben zu binomischen Formeln.

10 Zusammenfassung

In diesem Kurs haben wir die drei binomischen Formeln kennengelernt und uns ihre Herleitung angeschaut. Diese Formeln helfen dabei, Klammerterme schnell und einfach zu berechnen.

Was solltest du aus diesem Kurs mitnehmen? Die drei binomischen Formeln:

$(a + b)^{2} = a^{2} + 2 a b + b^{2}$

$(a - b)^{2} = a^{2} - 2 a b + b^{2}$
$(a + b) (a - b) = a^{2} - b^{2}$